Методы определение положения центра тяжести сложных фигур. Определение центра тяжести плоских фигур
Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).
Радиус-вектор этой точки

Рисунок 1.6
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.
Если удельный вес однородного тела γ , вес элементарной частицы тела
P k = γΔV k (P = γV ) подставить в формулу для определения r C , имеем
Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

Аналогично для координат центра тяжести однородной поверхности площадью S (рисунок 1.7, а)


Рисунок 1.7
Для координат центра тяжести однородной линии длиной L (рисунок 1.7, б)

Способы определения координат центра тяжести
Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:
1 Аналитический (путем интегрирования).
2 Метод симметрии . Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение . Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S 1 и S 2 (S = S 1 + S 2 ). Центры тяжести этих фигур находятся в точках C 1 (x 1 , y 1 ) и C 2 (x 2 , y 2 ) . Тогда координаты центра тяжести тела равны


Рисунок 1.8
5Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):


Рисунок 1.9
Центры тяжести простейших фигур

Рисунок 1.10
1 Треугольник
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).
DM = MB , CM = (1/3)AM .
2 Дуга окружности
Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е. y C = 0 .

dl – элемент дуги, dl = Rdφ , R – радиус окружности, x = Rcosφ , L = 2αR ,
Следовательно:
x C = R(sinα/α) .
3 Круговой сектор
Сектор радиуса R с центральным углом 2α имеет ось симметрии Ox , на которой находится центр тяжести (рисунок 1.10, в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3)R .
Центр тяжести сектора совпадает с центром тяжести дуги AB :
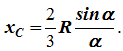
14. Способы задания движения точки.
При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.
При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t . Чтобы записать ее уравнение в явной форме, надо исключить из них t .
При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t) . Этим способом удобно пользоваться, если траектория точки заранее известна.
15. 1.2 Скорость точки
Рассмотрим перемещение точки за малый промежуток времени Δt :
![]()
средняя скорость точки за промежуток времени Dt . Скорость точки в данный момент времени


Скорость точки – это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета. Вектор скорости направлен по касательной к траектории точки в сторону движения.
Цель работы – определить центр тяжести сложной фигуры аналитическим и опытным путями.
Теоретическое обоснование. Материальные тела состоят из элементарных частиц, положение которых в пространстве определяется их координатами. Силы притяжения каждой частицы к Земле можно считать системой параллельных сил, равнодействующая этих сил называется силой тяжести тела или весом тела. Центр тяжести тела – это точка приложения силы тяжести.
Центр тяжести – это геометрическая точка, которая может быть расположена и вне тела (например, диск с отверстием, полый шар и т.п.). Большое практическое значение имеет определение центра тяжести тонких плоских однородных пластин. Их толщиной обычно можно пренебречь и считать, что центр тяжести расположен в плоскости. Если координатную плоскость xOy совместить с плоскостью фигуры, то положение центра тяжести определяется двумя координатами:
где - площадь части фигуры, ();
– координаты центра тяжести частей фигуры, мм (см).
| Сечение фигуры | А, мм 2 | X c ,мм | Y c , мм |
 | bh | b/2 | h/2 |
 | bh/2 | b/3 | h/3 |
 | R 2 a | ||
| При 2α = π πR 2 /2 |
Порядок проведения работы .
Начертить фигуру сложной формы, состоящую из 3-4 простых фигур (прямоугольник, треугольник, круг и т.п.) в масштабе 1:1 и проставить ее размеры.
Провести оси координат так, чтобы они охватывали всю фигуру, разбить сложную фигуру на простые части, определить площадь и координаты центра тяжести каждой простой фигуры относительно выбранной системы координат.
Вычислить координаты центра тяжести всей фигуры аналитически. Вырезать данную фигуру из тонкого картона или фанеры. Просверлить два отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.
Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в другой точке. Центр тяжести фигуры, найденный опытным путем, должны совпадать.
Определить координаты центра тяжести тонкой однородной пластины аналитически. Проверку произвести опытным путем
Алгоритм решения
1. Аналитический способ.
а) Чертеж вычертить в масштабе 1:1.
б) Сложную фигуру разбить на простые
в) Выбрать и провести оси координат (если фигура симметричная, то – по оси симметрии, в противном случае – по контору фигуры)
г) Вычислить площадь простых фигур и всей фигуры
д) Отметить положение центра тяжести каждой простой фигуры на чертеже
е) Вычислить координаты центра тяжести каждой фигуры
(по оси x и y)
ж) Вычислить координаты центра тяжести всей фигуры по формуле
з) Отметить положение центра тяжести на чертеже С (
2. Опытное определение.
Правильность решения задачи проверить опытным путем. Вырезать данную фигуру из тонкого картона или фанеры. Просверлить три отверстия, края отверстий должны быть гладкими, а диаметр отверстий несколько больше диаметра иглы для подвешивания фигуры.
Подвесить фигуру сначала в одной точке (отверстии), прочертить карандашом линию, совпадающую с нитью отвеса. То же повторить при подвешивании фигуры в других точках. Значение координат центра тяжести фигуры, найденных при подвешивании фигуры в двух точках: . Центр тяжести фигуры, найденный опытным путем, должны совпадать.
3.Заключение о положении центра тяжести при аналитическом и опытном определении.
Задание
Определить центр тяжести плоского сечения аналитическим и опытным путем.
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Пример выполнения
Задача
Определить координаты центра тяжести тонкой однородной пластины.

I Аналитический способ
1. Чертеж вычерчивается в масштабе (размеры обычно даны в мм)
2. Сложную фигуру разбиваем на простые.
1- Прямоугольник
2- Треугольник (прямоугольник)
3- Площадь полуокружности (ее нет, знак минус).
Находим положение центра тяжести простых фигур точек , и

3. Проводим оси координат как удобно и отмечаем начало координат т. О.
4. Вычисляем площади простых фигур и площадь всей фигуры. [размер в см]
(3. нет, знак -).
Площадь всей фигуры
5. Находим координату ц.т. , и на чертеже.
6. Вычисляем координаты точек C 1 , C 2 и C 3
7. Вычисляем координаты точки C
8. На чертеже отмечаем точку
II Опытным путем

Координаты центра тяжести опытным путем .
Контрольные вопросы.
1. Можно ли рассматривать силу тяжести тела как равнодействующую систему параллельных сил?
2. Может ли располагаться центр тяжести все самого тела?
3. В чем сущность опытного определения центра тяжести плоской фигуры?
4. Как определяется центр тяжести сложной фигуры, состоящей из нескольких простых фигур?
5. Как следует рационально производить разбиение фигуры сложной формы на простые фигуры при определении центра тяжести всей фигуры?
6. Какой знак имеет площадь отверстий в формуле для определения центра тяжести?
7. На пересечении каких линий треугольника находится его центр тяжести?
8. Если фигуру трудно разбить на небольшое число простых фигур, какой способ определения центра тяжести может дать наиболее быстрый ответ?
«Решение задач комплексного характера»
Цель работы: уметь решать задачи комплексного характера (кинематика, динамика)
Теоретическое обоснование: Скорость есть кинематическая мера движения точки, характеризующая быстроту изменения ее положения. Скорость точки представляет собой вектор, характеризующий быстроту и направление движения точки в данный момент времени. При задании движения точки уравнениями проекции скорости на оси декартовых координат равны:
Модуль скорости точки определяется по формуле
Направление скорости определяется направляющими косинусами:

Характеристикой быстроты изменения скорости является ускорение а. Ускорение точки равно производной от вектора скорости по времени:
При задании движения точки уравнения проекции ускорения на координатные оси равны:

Модуль ускорения:

Модуль полного ускорения
Модуль касательного ускорения определяется по формуле

Модуль нормального ускорения определяется по формуле
где – радиус кривизны траектории в данной точке.
Направление ускорения определяется направляющими косинусами

Уравнение вращательного движения твердого тела вокруг неподвижной оси имеет вид
Угловая скорость тела:
Иногда угловую скорость характеризуют числом оборотов в минуту и обозначают буквой . Зависимость между и имеет вид
Угловое ускорение тела:

Сила, равная произведению массы данной точке на ее ускорение и направление в сторону прямопротивоположную ускорению точки, называется силой инерции.
Мощностью называется работа, выполненная силой в единицу времени
Основное уравнение динамики для вращательного движения
– момент инерции тела относительно оси вращения, есть сумма произведений масс материальных точек на квадрат расстояний их до этой оси
Задание
Тело массой m с помощью троса, наматываемого на барабан диаметром d, перемещается вверх или вниз по наклонной плоскости с углом наклона α. Уравнение движения тела S=f(t), уравнение вращения барабана , где S в метрах; φ - в радианах; t – в секундах. P и ω - соответственно мощность и угловая скорость на валу барабана в момент конца разгона или начала торможения. Время t 1 – время разгона (из состояния покоя до заданной скорости) или торможения (от заданной скорости до остановки). Коэффициент трения скольжения между телом и плоскостью –f. Потерями на трение на барабане, а также массой барабана пренебречь. При решении задач принять g=10 м/с 2
| № вар | α, град | Закон движения | Напр движ | m, кг | t 1 , c | d, м | P, кВт | , рад/с | f | Опред. величины |
| S=0,8t 2 | Вниз | - | - | 0,20 | 4,0 | 0,20 | m,t 1 | |||
| φ=4t 2 | Вниз | 1,0 | 0,30 | - | - | 0,16 | P,ω | |||
| S=1,5t-t 2 | вверх | - | - | - | 4,5 | 0,20 | m, d | |||
| ω=15t-15t 2 | вверх | - | - | 0,20 | 3,0 | - | 0,14 | m,ω | ||
| S=0,5t 2 | Вниз | - | - | 1,76 | 0,20 | d,t 1 | ||||
| S=1,5t 2 | Вниз | - | 0,6 | 0,24 | 9,9 | - | 0,10 | m,ω | ||
| S=0,9t 2 | Вниз | - | 0,18 | - | 0,20 | P, t 1 | ||||
| φ=10t 2 | Вниз | - | 0,20 | 1,92 | - | 0,20 | P, t 1 | |||
| S=t-1,25t 2 | вверх | - | - | - | 0,25 | P,d | ||||
| φ=8t-20t 2 | вверх | - | 0,20 | - | - | 0,14 | P, ω |
Пример выполнения
Задача 1 (рисунок 1).
Решение 1. Прямолинейное движение (рисунок 1, а). Точка, двигавшаяся равномерно, в некоторый момент времени получила новый закон движения , и через некоторый промежуток времени остановилась. Определить все кинематические характеристики движения точки для двух случаев; а) движение по прямолинейной траектории; б) движение по криволинейной траектории постоянного радиуса кривизны r=100см
Рисунок 1 (а).
Закон изменения скорости точки
Начальную скорость точки найдем из условия:
Время торможения до остановки найдем из условия:
при , отсюда .
Закон движения точки в период равномерного движения
Расстояние, пройденное точкой по траектории за период торможения,
Закон изменения касательного ускорения точки
откуда следует, что в период торможения точка двигалась равнозамедленно, так как касательное ускорение отрицательно и по значению постоянно.
Нормальное ускорение точки на прямолинейной траектории движения равно нулю, т.е. .
Решение 2. Криволинейное движение (рисунок 1, б).
Рисунок 1 (б)

В этом случае по сравнению со случаем прямолинейного движения остаются без изменения все кинематические характеристики, за исключением нормального ускорения.
Закон изменения нормального ускорения точки
Нормальное ускорение точки в начальный момент торможения
Принятая на чертеже нумерация положений точки на траектории: 1 – текущее положение точки в равномерном движении до начала торможения; 2 – положение точки в момент начала торможения; 3 – текущее положение точки в период торможения; 4 – конечное положение точки.
Задача 2.
Груз (рис. 2, а) поднимается с помощью барабанной лебедки. Диаметр барабана d=0,3м, а закон его вращения .
Разгон барабана длился до угловой скорости . Определить все кинематические характеристики движения барабана и груза.


Решение . Закон изменения угловой скорости барабана . Начальную угловую скорость найдем из условия: ; следовательно, разгон начался из состояния покоя. Время разгона найдем из условия: . Угол поворота барабана за период разгона .
Закон изменения углового ускорения барабана , отсюда следует, что в период разгона барабан вращался равноускоренно.
Кинематические характеристики груза равны соответствующим характеристикам любой точки тягового троса, а значит, и точки A, лежащей на ободе барабана (рис. 2, б). Как известно, линейные характеристики точки вращающегося тела определяются через его угловые характеристики.
Расстояние, пройденное грузом за период разгона, . Скорость груза в конце разгона .
Ускорение груза .
Закон движения груза .
Расстояние, скорость и ускорение груза можно было определить и иначе, через найденный закон движения груза:
Задача 3.
Груз, перемещавшийся равномерно вверх по наклонной опорной плоскости, в некоторый момент времени получил торможение в соответствии с новым законом движения ![]() , где s – в метрах и t – в секундах. Масса груза m = 100кг, коэффициент трения скольжения между грузом и плоскостью f=0,25. Определить силу F и мощность на тяговом тросе для двух моментов времени: а) равномерное движение до начала торможения;
, где s – в метрах и t – в секундах. Масса груза m = 100кг, коэффициент трения скольжения между грузом и плоскостью f=0,25. Определить силу F и мощность на тяговом тросе для двух моментов времени: а) равномерное движение до начала торможения;
б) начальный момент торможения. При расчёте принять g=10 м/ .
Решение. Определяем кинематические характеристики движения груза.
Закон изменения скорости груза
Начальная скорость груза (при t=0)
Ускорение груза
Так как ускорение отрицательно, то движение – замедленное.
1. Равномерное движение груза.

Для определения движущей силы F рассматриваем равновесие груза, на который действует система сходящихся сил: сила на тросе F, сила тяжести груза G=mg, нормальная реакция опорной поверхности N и сила трения , направленная навстречу движению тела. По закону трения, . Выбираем направление координатных осей, как показано на чертеже, и составляем два уравнения равновесия для груза:
Мощность на тросе до начала торможения определим по известной формуле
Где м/с.
2. Замедленное движение груза.

Как известно, при неравномерном поступательном движении тела система действующих на него сил по направлению движения не является уравновешенной. Согласно принципу Даламбера (метод кинетостатики), тело в этом случае можно считать находящимся в условном равновесии, если ко всем действующим на него силам добавить силу инерции , вектор которой направлен противоположно вектору ускорения. Вектор ускорения в нашем случае направлен противоположно вектору скорости, так как груз движется замедленно. Составляем два уравнения равновесия для груза:
Мощность на тросе в момент начала торможения
Контрольные вопросы.
1. Как определить численное значение и направление скорости точки в данный момент?
2. Что характеризует нормальная и касательная составляющие полного ускорения?
3. Как перейти от выражения угловой скорости в мин -1 к ее выражению рад/с?
4. Что называют массой тела? Назовите единицу измерения массы
5. При каком движении материальной точки возникает сила инерции? Чему равно ее численное значение, как она направлена?
6. Сформулируйте принцип Даламбера
7. Возникает ли сила инерции при равномерном криволинейном движении материальной точки?
8. Что такое вращающий момент?
9. Как выражается зависимость между вращающим моментом и угловой скорости при данной передаваемой мощности?
10. Основное уравнение динамики для вращательного движения.
Практическая работа №7
«Расчет конструкций на прочность»
Цель работы: определять прочность, размеры сечения и допускаемую нагрузку
Теоретическое обоснование.
Зная силовые факторы и геометрические характеристики сечения при деформации растяжение (сжатие), мы можем определить напряжение по формулам. А что бы понять, выдержит ли наша деталь (вал, шестерня и т. д.) внешнюю нагрузку. Необходимо эту величину сравнить с допустимым напряжением.
Итак, уравнение статической прочности
На его основании решают 3 типа задач:
1) проверка прочности
2) определение размеров сечения
3) определение допускаемой нагрузки
Итак, уравнение статической жёсткости
На его основании решают также 3 типа задач
Уравнение статической прочности при растяжении (сжатии)
![]()
1) Первый тип - проверка прочности
![]() ,
,
т. е. решаем левую часть и сравниваем с допускаемым напряжением.
2) Второй тип - определение размеров сечения
![]()
из правой части площадь поперечного сечения
 Сечение круг
Сечение круг
отсюда диаметр d
Сечение прямоугольник

Сечение квадрат

A = a² (мм²)
Сечение полукруг

Сечения швеллер, двутавр, уголок и т. д.
Значения площади - из таблицы, принимается по ГОСТ
3) Третий тип - определение допустимой нагрузки;
![]()
принимается в меньшую сторону, целое число
ЗАДАНИЕ
Задача
А) Проверка прочности (проверочный расчет)
Для заданного бруса построить эпюру продольных сил и проверить прочность на обоих участках. Для материала бруса (сталь Ст3) принять ![]()
![]()
| № варианта | ||||||
| 12,5 | 5,3 | - | - | |||
| 2,3 | - | - | ||||
| 4,2 | - | - |
Б) Подбор сечения (проектный расчет)
Для заданного бруса построить эпюру продольных сил и определить размеры поперечного сечения на обоих участках. Для материала бруса (сталь Ст3) принять
| № варианта | ||
| 1,9 | 2,5 | |
| 2,8 | 1,9 | |
| 3,2 |
В) Определение допускаемой продольной силы
Для заданного бруса определить допускаемые значения нагрузок и ,
построить эпюру продольных сил. Для материала бруса (сталь Ст3) принять . При решении задачи считать, что на обоих участках бруса вид нагружения одинаков.
| № варианта | ||||
| - | - | |||
| - | - | |||
| - | - |

 Пример выполнения задания
Пример выполнения задания
Задача 1 (рисунок 1).
Проверить прочность колонны, выполненной из двутавровых профилей заданного размера. Для материала колонны (сталь Ст3) принять допускаемые напряжения при растяжении ![]() и при сжатии
и при сжатии ![]() . В случае наличия перезагрузки или значительной недогрузки подобрать размеры двутавров, обеспечивающие оптимальную прочность колонны.
. В случае наличия перезагрузки или значительной недогрузки подобрать размеры двутавров, обеспечивающие оптимальную прочность колонны.
Решение.
Заданный брус имеет два участка 1, 2. Границами участков являются сечения, в которых приложены внешние силы. Так как силы, нагружающие брус, расположены по его центральной продольной оси, то в поперечных сечениях возникает лишь один внутренний силовой фактор – продольная сила , т.е. имеет место растяжение (сжатие) бруса.

Для определения продольной силы применяем метод сечений метод сечений. Проводя мысленно сечение в пределах каждого из участков, будем отбрасывать нижнюю закрепленную часть бруса и оставлять для рассмотрения верхнюю часть. На участке 1 продольная сила постоянна и равна
Знак минус указывает на то, что на обоих участках брус сжат.
Строим эпюру продольных сил . Проведя параллельно оси бруса базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения . Как видим, эпюра оказалась очерчена прямыми линиями, параллельными базовой.
Выполняем проверку прочности бруса, т.е. определяем расчетное напряжение (для каждого участка в отдельности) и сравниваем его с допускаемым. Для этого используем условие прочности при сжатии
![]()
где площадь является геометрической характеристикой прочности поперечного сечения. Из таблицы прокатной стали берем:
для двутавра
для двутавра
Проверка прочности:
Значения продольных сил взяты по абсолютной величине.
Прочность бруса обеспечена, однако имеет место значительная (более 25%) недогрузка, что недопустимо вследствие перерасхода материала.
Из условия прочности определяем новые размеры двутавра для каждого из участков бруса:
Отсюда требуемая площадь
По таблице ГОСТа выбираем двутавр № 16 , для которого ;
Отсюда требуемая площадь
По таблице ГОСТа выбираем двутавр №24, для которого ;
При выбранных размерах двутавров также имеет место недогрузка, однако незначительная (менее 5%)
Задача №2.
Для бруса с заданными размерами поперечного сечения определить допускаемые значения нагрузок и . Для материала бруса (сталь Ст3) принять допускаемые напряжения при растяжении ![]() и при сжатии
и при сжатии ![]() .
.

Решение.
Заданный брус имеет два участка 1, 2. Имеет место растяжение (сжатие) бруса.
Применяя метод сечений, определяем продольную силу , выражая ее через искомые силы и . Проводя в пределах каждого из участков сечение, будем отбрасывать левую часть бруса и оставлять для рассмотрения правую часть. На участке 1 продольная сила постоянна и равна
На участке 2 продольная сила также постоянна и равна
Знак плюс указывает на то, что на обоих участкахбрус растянут.
Строим эпюру продольных сил . Эпюра очерчена прямыми линиями, параллельными базовой.

Из условия прочности при растяжении определяем допускаемые значения нагрузок и предварительно вычислив площади заданных поперечных сечений:
![]()
![]()
Контрольные вопросы.
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Запишите условие прочности при растяжении и сжатии.
3. Как назначают знаки продольной силы и нормального напряжения?
4. Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?
5. Различаются ли условия прочности при расчете на растяжение и расчете на сжатие?
6. В каких единицах измеряется напряжение?
7. Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?
8. В чем разница между предельным и допускаемым напряжением?
Практическая работа №8
«Решение задач по определению главных центральных моментов инерции плоских геометрических фигур»
Цель работы: определить аналитическим путем моменты инерции плоских тел сложной формы
Теоретическое обоснование. Координаты центра тяжести сечения можно выразить через статический момент:
![]()
где относительно оси Оx
относительно оси Оy
Статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние ее центра тяжести до этой оси. Статический момент имеет размерность . Статический момент может быть величиной положительной, отрицательной и равен нулю (относительно любой центральной оси).
Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений или интеграл элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в плоскости рассматриваемого сечения
Осевой момент инерции выражается в единицах - . Осевой момент инерции- величина всегда положительная и не равна нулю.
Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.
Момент инерции относительно какой-либо оси равен центра
Которого требуется определить, однородное и имеет простую форму – прямоугольную, круглую, шарообразную, цилиндрическую, квадратную, и у него есть центр симметрии, в подобном случае центр тяжести совпадает с центром симметрии.
Для однородного стержня центр тяжести расположен в его середине, то есть в его геометрическом центре. Точно такой же результат получается и для однородного круглого диска. Его центр тяжести лежит в точке пересечения диаметров круга. Поэтому и центр тяжести окажется в его центре, вне точек самого обруча. Найдите центр тяжести однородного шара – он расположен в геометрическом центре сферы. Центр тяжести однородного окажется на пересечении его диагоналей.
Если тело имеет произвольную форму, если оно неоднородно, скажем, имеет выемки, рассчитать положение сложно. Разберитесь, где у такого тела располагается точка пересечения всех сил тяжести, которые действуют на эту фигуру при ее переворачивании. Найти данную точку проще всего опытным путем, воспользовавшись способом свободного подвешивания тела на нити.
Последовательно прикрепляйте тело к нити за разные точки. При равновесии центр тяжести тела должен лежать на линии, совпадающей с линией нити, иначе сила тяжести привела бы тело в движение.
При помощи линейки и карандаша прочертите вертикальные прямые, совпадающие с направлением нитей, которые были закреплены в разных точках. В зависимости от сложности формы тела понадобится провести две-три линии. Все они должны пересечься в одной точке. Эта точка и будет центром тяжести данного тела, потому что центр тяжести должен одновременно находиться на всех подобных прямых.
Определите с помощью способа подвешивания центр тяжести как плоской фигуры, так и более сложного тела, форма которого может изменяться. Например, два бруска, соединенные шарниром, в разложенном состоянии имеют центр тяжести в геометрическом центре, а в согнутом – их центр тяжести вне этих брусков.
Источники:
- Центр тяжести тел
- как определить центр тяжести тела
- Вычисление координат центра тяжести плоской
Еще в школе на уроках физики мы впервые знакомимся с таким понятием, как центр тяжести. Задача не из легких, но хорошо объяснима и понятна. Не только юному физику понадобится знать определение центра тяжести. И если вы столкнулись с данной задачей, стоит прибегнуть к подсказкам и напоминаниям, дабы обновить свою память.
Инструкция
Проштудировав учебники физики, механики, словари или энциклопедии, вы наткнетесь на центра тяжести или как называют центр масс.
В разных науках немного разные определения, но суть, фактически, не теряется. Центр тяжести всегда находится в центре симметрии тела. Для более наглядного понятия «центр тяжести (или по другому называют центр масс) - это , что неизменно связанна с твердым телом. Через неё проходит равнодействующая сил тяжести, действующие на частицу данного тела при любом его положение».
Если центр тяжести твердого тела - это точка, значит она должна иметь свои координаты.
Для определения важно знать координаты по x, y, z, i-той части тела и вес, обозначающийся буквой - p.
Рассмотрим пример задачи.
Даны два тела различных масс m1 и m2,на которые действуют разные весовые силы (как изображено на рисунке). Записав веса:
P1= m1*g, Р2= m2*g;
Центр тяжести находится между двумя массами. И если все тело подвесить в т.О, наступит значение равновесие, то есть эти перестанут перевешивать друг друга.
Разнообразные геометрические фигуры имеют физические и расчеты по поводу центра тяжести. К каждому свой подход и свой метод.
Рассматривая диск, уточняем, что центр тяжести находится внутри него, точнее диаметров (как показано на рисунке в т.С - точка пересечение диаметров). Таким же способом находят центры параллелепипеда или однородного шара.
Представленный диск и два тела с массами m1 и m2 - однородной массы и правильной формы. Здесь можно отметить, что искомый нами центр тяжести находится внутри этих предметов. Однако, в телах с неоднородной массой и неправильной формы центр может находится за . Чувствуете сами, что задача уже становится сложнее.
Равновесием с точки зрения экономической науки называется такое состояние системы, когда каждый из участников рынка не желает изменить свое поведение. Рыночное равновесие определяется, таким образом, как ситуация, когда продавцами предлагается для продажи точно такое количество товара, какое покупатели желают приобрести. Отыскание точки равновесия заключается в построении некоторой идеальной модели рыночного поведения участников экономических отношений.

Инструкция
Воспользуйтесь для нахождения точки равновесия понятиями о спроса и . Это поможет определить, при каком уровне цены обе функции будут иметь равные значения. Спрос характеризует покупателей приобрести товар, а – готовность производителя этот товар продать.
Выразите функции спроса и предложения при помощи таблицы, состоящей из трех столбцов (см. Рис. 1). Первая колонка цифр будет включать значения цены, например, в за единицу товара. Второй столбец определяет объем спроса, а третий – объем предложения за некоторый заранее определенный период.

Используйте для нахождения рыночного равновесия графическое отображение спроса и предложения. Данные из таблицы, аналогичной приведенной выше, перенесите в пространство двух осей, одна из которых (P) отображает уровень цены, а вторая (Q) – количество единиц товара.
Соедините линиями точки, отражающие изменение параметров в каждом столбце. В результате вы получите два графика D и S, пересекающихся в некоторой точке. Кривая D является отражением потребительского спроса на товар, а кривая S картину предложения того же товара на рынке.
Отметьте точку пересечения двух кривых как A. Эта общая точка демонстрирует равновесное значение количества товара и цены на него в данном сегменте рынка. Такое графическое изображение точки равновесия картину спроса и предложения более объемной и наглядной.
Видео по теме
Центр тяжести любого геометрического предмета – точка пересечения всех сил тяжести, действующих на фигуру при любом изменении ее положения. Иногда эта отметка может не совпадать с телом, находясь вне его границ.
Как найти центр тяжести
Автор : Возьмем тело произвольной формы. Можно ли подвесить его на нити так, чтобы оно после подвешивания сохранило свое положение (т.е. не стало поворачиваться) при любой начальной ориентации (рис. 27.1)?
Иными словами, существует ли такая точка, относительно которой сумма моментов сил тяжести, действующих на различные части тела, была бы равна нулю при любой ориентации тела в пространстве?
Читатель : По-моему, да. Такая точка называется центром тяжести тела.
Доказательство. Для простоты рассмотрим тело в виде плоской пластины произвольной формы произвольным образом ориентированное в пространстве (рис. 27.2). Возьмем систему координат х 0у с началом в центре масс – точке С , тогда х С = 0, у С = 0.
 Представим это тело в виде совокупности большого числа точечных масс m i
, положение каждой из которых задается радиусом-вектором .
Представим это тело в виде совокупности большого числа точечных масс m i
, положение каждой из которых задается радиусом-вектором .
По определению центра масс , а координата х С = .
Так как в принятой нами системе координат х С = 0, то . Умножим это равенство на g и получим
Как видно из рис. 27.2, |x i | – это плечо силы . Причем если х i > 0, то момент силы M i > 0, а если х j < 0, то M j < 0, поэтому с учетом знака можно утверждать, что для любого x i момент силы будет равен M i = m i gx i . Тогда равенство (1) эквивалентно равенству , где M i – момент силы тяжести . А это значит, что при произвольной ориентации тела сумма моментов сил тяжести, действующих на тело, будет равна нулю относительно его центра масс.
Чтобы рассматриваемое нами тело находилось в равновесии, к нему необходимо приложить в точке С силу Т = mg , направленную вертикально вверх. Момент этой силы относительно точки С равен нулю.
Поскольку наши рассуждения никак не зависели от того, как именно ориентировано тело в пространстве, мы доказали, что центр тяжести совпадает с центром масс, что и требовалось доказать.
Задача 27.1. Найти центр тяжести невесомого стержня длины l , на концах которого укреплены две точечные массы т 1 и т 2 .
| т 1 т 2 l | Решение. Будем искать не центр тяжести, а центр масс (так как это одно и то же). Введем ось х
(рис. 27.3).
|
| х С = ? | |
Ответ : на расстоянии от массы т 1 .
СТОП! Решите самостоятельно: В1–В3.
Утверждение 1. Если однородное плоское тело имеет ось симметрии, центр тяжести находится на этой оси.
Действительно, для всякой точечной массы m i , расположенной справа от оси симметрии, найдется такая же точечная масса , расположенная симметрично относительно первой (рис. 27.4). При этом сумма моментов сил .
Поскольку все тело можно представить разбитым на подобные пары точек, то суммарный момент сил тяжести относительно любой точки, лежащей на оси симметрии равен нулю, а значит, на этой оси находится и центр тяжести тела. Отсюда следует важный вывод: если тело имеет несколько осей симметрии, то центр тяжести лежит на пересечении этих осей (рис. 27.5).
Рис. 27.5 
Утверждение 2 . Если два тела массами т 1 и т 2 соединены в одно, то центр тяжести такого тела будет лежать на отрезке прямой, соединяющей центры тяжести первого и второго тела (рис. 27.6).
Рис. 27.6 ![]() Рис. 27.7
Рис. 27.7
Доказательство. Расположим составное тело так, чтобы отрезок, соединяющий центры тяжести тел был вертикальным. Тогда сумма моментов сил тяжести первого тела относительно точки С 1 равна нулю, и сумма моментов сил тяжести второго тела относительно точки С 2 равна нулю (рис. 27.7).
Заметим, что плечо силы тяжести любой точечной массы т i одно и то же относительно любой точки, лежащей на отрезке С 1 С 2 , а значит, и момент силы тяжести относительно любой точки, лежащей на отрезке С 1 С 2 , один и тот же. Следовательно, сил тяжести всего тела равен нулю относительно любой точки отрезка С 1 С 2 . Таким образом, центр тяжести составного тела лежит на отрезке С 1 С 2 .
Из утверждения 2 следует важный практический вывод, который четко сформулирован в виде инструкции.
Инструкция,
как искать центр тяжести твердого тела, если его можно разбить
на части, положения центров тяжести каждой из которых известно
1. Следует заменить каждую часть массой, расположенной в центре тяжести этой части.
2. Найти центр масс (а это то же самое, что и центр тяжести) полученной системы точечных масс, выбрав удобную систему координат х 0у , по формулам:
В самом деле, расположим составное тело так, чтобы отрезок С 1 С 2 был горизонтальным, и подвесим его на нитях в точках С 1 и С 2 (рис. 27.8,а ). Ясно, что тело будет находиться в равновесии. И это равновесие не нарушится, если мы заменим каждое тело точечными массами т 1 и т 2 (рис. 27.8,б ).
 Рис. 27.8
Рис. 27.8
СТОП! Решите самостоятельно: С3.
Задача 27.2. В двух вершинах равностороннего треугольника помещены шарики массы т каждый. В третьей вершине помещен шарик массы 2т (рис. 27.9,а ). Сторона треугольника а . Определить центр тяжести этой системы.
| т 2т а |  Рис. 27.9
Рис. 27.9
|
| х С = ? у С = ? | |
Решение . Введем систему координат х 0у (рис. 27.9,б ). Тогда
![]() ,
,
 .
.
Ответ : х С = а /2; ; центр тяжести лежит на половине высоты АD .
Перед тем, как найти центр тяжести простых фигур, таких которые обладают прямоугольной, круглой, шарообразной или цилиндрической, а также квадратной формой, необходимо знать, в какой точке находится центр симметрии конкретной фигуру. Поскольку в данных случаях, центр тяжести будет совпадать с центром симметрии.
Центр тяжести однородного стержня располагается в его геометрическом центре. Если необходимо определить центр тяжести круглого диска однородной структуры, то для начала найдите точку пересечения диаметров круга. Она и будет центром тяжести данного тела. Рассматривая такие фигуры, как шар, обруч и однородный прямоугольный параллелепипед, можно с уверенностью сказать, что центр тяжести обруча будет находиться в центре фигуры, но вне ее точек, центр тяжести шара - геометрический центр сферы, и в последнем случае, центром тяжестью считается пересечение диагоналей прямоугольного параллелепипеда.
Центр тяжести неоднородных тел
Чтобы найти координаты центра тяжести, как и сам центр тяжести неоднородного тела, необходимо разобраться, на каком отрезке данного тела располагается точка, в которой пересекаются все силы тяжести, действующие на фигуру, если ее переворачивать. На практике для нахождения такой точки подвешивают тело на нить, постепенно меняя точки прикрепления нити к телу. В том случае, когда тело находится в равновесии, то центр тяжести тела будет лежать на линии, которая совпадает с линией нити. В противном случае сила тяжести приводит тело в движение.
Возьмите карандаш и линейку, начертите вертикальные прямые, которые визуально будут совпадать с нитевыми направлениями (нити, закрепляемые в различных точках тела). Если форма тела достаточно сложная, то проведите несколько линий, которые будут пересекаться в одной точке. Она и станет центром тяжести для тела, над которым вы производили опыт.
Центр тяжести треугольника
Для нахождения центра тяжести треугольника, необходимо нарисовать треугольник – фигуру, состоящую из трех отрезков, соединенных между собой в трех точках. Перед тем, как найти центр тяжести фигуры, необходимо, используя линейку, измерить длину одной стороны треугольника. В середине стороны поставьте отметку, после чего противоположную вершину и середину отрезка соедините линией, которая называется медианой. Тот же самый алгоритм повторите со второй стороной треугольника, а затем и с третьей. Результатом вашей работы станут три медианы, которые пересекаются в одной точке, которая будет являться центром тяжести треугольника.
Если перед вами стоит задача, касающаяся того, как найти центр тяжести тела в форме равностороннего треугольника, то необходимо из каждой вершины провести высоту с помощью прямоугольной линейки. Центр тяжести в равностороннем треугольнике будет находиться на пересечении высот, медиан и биссектрис, поскольку одни и те же отрезки одновременно являются высотами, медианами и биссектрисами.
Координаты центра тяжести треугольника
Перед тем, как найти центр тяжести треугольника и его координаты, рассмотрим подробнее саму фигуру. Это однородная треугольная пластина, с вершинами А, В, С и соответственно, координатами: для вершины А - x1 и y1; для вершины В - x2 и y2; для вершины С - x3 и y3. При нахождении координат центра тяжести мы не будем учитывать толщину треугольной пластины. На рисунке ясно видно, что центр тяжести треугольника обозначен буквой Е – для его нахождения мы провели три медианы, на пересечении которых и поставили точку Е. Она имеет свои координаты: xE и yE.
Один конец медианы, проведенной из вершины А к отрезку В, обладает координатами x 1 , y 1 , (это точка А), а вторые координаты медианы получаем, исходя из того, что точка D (второй конец медианы) стоит посередине отрезка BC. Концы данного отрезка обладают известными нам координатами: B(x 2 , y 2) и C(x 3 , y 3). Координаты точки D обозначаем xD и yD . Исходя из следующих формул:
х=(Х1+Х2)/2; у=(У1+У2)/2
Определяем координаты середины отрезка. Получим следующий результат:
хd=(Х2+Х3)/2; уd=(У2+У3)/2;
D *((Х2+Х3)/2 , (У2+У3)/2).
Мы знаем, какие координаты характерны для концов отрезка АД. Также нам известны координаты точки Е, то есть, центра тяжести треугольной пластины. Также мы знаем, что центр тяжести расположен посередине отрезка АД. Теперь, применяя формулы и известные нам данные, мы можем найти координаты центра тяжести.
Таким образом, можно найти координаты центра тяжести треугольника, вернее, координаты центра тяжести треугольной пластины, учитывая то, что ее толщина нам неизвестна. Они равны среднему арифметическому однородных координат вершин треугольной пластины.